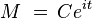Comparación de alternativas con vidas útiles iguales.
El proceso del método del Valor Presente Neto es el mismo que se uso para encontrar el valor de P, es decir la cantidad en el presente.
Ejemplo:
1. Cierta empresa tiene que decidir entre 2 activos (equipos para un proceso de producción). La duración de estos activos se estima en 5 años.
Si la trema de la empresa es del 25 %, ¿Qué activo recomendaría adquirir?
Solución (miles de pesos):
VPNA = -16 + 4.5 (P/F, 25%, 1) + 5.5 (P/F, 25%, 2) + 6 (P/F, 25%, 3) + 7 (P/F, 25%,4) + 12 (P/F, 25%, 5). VPNA = 0.99136 miles de pesos.
VPNB = -15 +6.5 (P/F, 25%,1) +7 (P/F, 25%, 2) + 7.5 (P/F, 25 %, 3) + 8 (P/F, 25%, 4) + 12 (P/F, 25%, 5). VPNB = 5.72896 miles de pesos.
Como VPNA > VPNB por lo tanto se recomienda adquirir el activo B.
COMPARACION DE ALTERNATIVAS CON VIDAS IGUALES
Tienen capacidades de alternativas idénticas para un mismo periodo de tiempo
Guía para seleccionar alternativas:
1. Para una sola alternativa: Si el VP es > o = a “0”, entonces la Tasa de Interés es lograda o excedida y la alternativa es financieramente viable.
2. Para 2 o más alternativas: Se selecciona la alternativa menos negativa o la más positiva.
Comparación de Alternativas con vidas iguales
Ejercicios:
1. Realice una comparación del valor presente de las maquinas y seleccione lamedor para las cuáles se muestran los costos:
Concepto Eléctrico Gas Solar
Costo inicial 2500 3500 6000
Costo Anual de operaciones 900 700 50
Valor de salvamento 200 350 100
Vida en años 5 5 5
2. Un agente desea comprar un auto y estima: Costo inicial=$10000, Valor comercial= $500 dentro de 4 años, el mantenimiento anual y seguro= $1500 y le ingreso anual adicional debido a la capacidad de viaje= $5000, ¿Podrá el agente obtener una tasa de retorno del 20% anual de su compra
http://itvh-fea-ingenieria-economica.blogspot.mx/2012/09/unidad-2-metodos-de-evaluacion-y.html

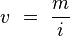
![M\,=\,C\left[ \left(1+ \frac{i}{m}\right)^v \, \right]^{it}](https://upload.wikimedia.org/math/e/6/4/e64bef6984b33ec3ad1dcc58048bd669.png)
![\lim_{v \to \, \infty}\,C\left[ \left(1+ \frac{i}{m}\right)^v \, \right]^{it} \ = \,C e^{it}](https://upload.wikimedia.org/math/f/f/7/ff7b8095e6d3b240aebeff3261222281.png)
 = Tasa Efectiva
= Tasa Efectiva = Periodicidad
= Periodicidad = Tiempo
= Tiempo