Tasa de interes efectiva para capitalizacion continua
La Capitalización Continua es una formula que nos ayuda calcular el valor presente y el valor futuro de cierta cantidad con intereses que se ven acumulando es decir, los interese que se ganan en un periodo más la cantidad inicial, se volverán a invertir en el siguiente periodo y así sucesivamente, es por esto que se considera un tipo de capitalización compuesta.
La diferencia radica en que los periodos de capitalización son demasiado cortos, casi instantáneos es por esto que se le llama "Capitalización Continua" por que es casi continua la capitalización de intereses.
Si se tiene una tasa nominal constante y la capitalización es más frecuente, el monto compuesto (capital + intereses) aumenta. Esto quiere decir que entre más rápido es la capitalización de los intereses, mayor será el monto esperado. La periodicidad instantánea sería cuando "m" tiende a infinito. Si "m" tiende a infinito también "v".
Las fórmulas para obtener el valor futuro y presente de la capitalización continua son:
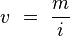
![M\,=\,C\left[ \left(1+ \frac{i}{m}\right)^v \, \right]^{it}](https://upload.wikimedia.org/math/e/6/4/e64bef6984b33ec3ad1dcc58048bd669.png)
![\lim_{v \to \, \infty}\,C\left[ \left(1+ \frac{i}{m}\right)^v \, \right]^{it} \ = \,C e^{it}](https://upload.wikimedia.org/math/f/f/7/ff7b8095e6d3b240aebeff3261222281.png)
Donde:
- M = Valor Futuro
- C = Valor Presente
= Tasa Efectiva
= Periodicidad
= Tiempo
Por lo tanto simplificando la fórmula, el valor futuro y el valor presente calculado a una tasa instantánea o de capitalización continua será:2
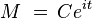
La nomenclatura se respeta siendo la misma de arriba.
https://es.wikipedia.org/wiki/Capitalizaci%C3%B3n_continua
No hay comentarios.:
Publicar un comentario